The Sundials CVODE suite is an established, widely used C-library dedicated to solving ODEs. It provides variable-order, variable-step integration routines for stiff and non-stiff systems based on multi-step methods. In the following I will show a basic performance comparison of CVODE with odeint using the Lorenz model as a simple example system.

CVODE

For our future plans to increase odeint's functionality towards stiff systems we decided to get some inspiration from CVODE to provide comparable functionality. Therefore, I started playing around with CVODE a bit and implemented a simple simulation of the famous Lorenz system. The implementation in CVODE is slightly tedious for someone used to C++, but rather straight-forward. Like many other C-libraries (GSL, Numerical Recipes Codes), CVODE introduces its own vector types (NVector) for which element access is realized by Macros, which really hurts readability in my opinion. For example, the function defining the Lorenz system for CVODE reads as:

int lorenz(realtype t, N_Vector y, N_Vector y_dot, void *params)
{
    // lorenz equations
    NV_Ith_S(y_dot, 0) = SIGMA * ( NV_Ith_S(y, 1) - NV_Ith_S(y, 0) );
    NV_Ith_S(y_dot, 1) = R * NV_Ith_S(y, 0) - NV_Ith_S(y, 1) - NV_Ith_S(y, 0) * NV_Ith_S(y, 2);
    NV_Ith_S(y_dot, 2) = -B * NV_Ith_S(y, 2) + NV_Ith_S(y, 0) * NV_Ith_S(y, 1);

    return 0;
}

However, having implemented this simulation I decided to use this as basis for a quick performance comparison between odeint and CVODE. The test run consists of integrating a trajectory of the Lorenz system starting at t0=0 until t1=100 with a maximal error of 10^-6. This is then repeated 100 times to get somewhat reliable results. The source codes for both implementations can be found on Github.

Runtime Results

Before timing the simulations I should note a few things. As said above, CVODE uses an variable-order, variable-step Adams-Moulton method for this kind of non-stiff problem, while in odeint I used a Runge-Kutta-Dopri5 algorithm, which has fixed order 5, but variable step-size. A priori, it is not clear which of the two methods are more suitable for the problem at hand. Typically, the Adams-Moulton method requires less rhs function evaluations then the Dopri-5, but it contains fixed point iterations which is more complicated than the simple explicit computations in the Runge-Kutta stepper. Furthermore, the general advantage of odeint is that it is header only, which gives the compiler much better optimization opportunities than for the pre-compiled CVODE.

The source codes can be found here and are compiled with gcc/g++ 4.8.4 using -Ofast to get best performance and run on my Intel Core i5-3210M CPU @ 2.50GHz. Below are the results for my first basic performance tests:

CVODE:

odeint:

This is highly surprising! Although the odeint algorithm requires almost twice as many calls to the lorenz function, it overall runs about 30 times faster than CVODE (0.07s vs 2.2s). However, this is not a fair comparison, as it might be that the Adams-Moulton method is inferior to the simpler Runge-Kutta-Dopri5 for such a small and simple system as the Lorenz model.

Measuring Flops

Let's try to get a deeper understanding of what's going on by actually mesuring the CPU performance in terms of Flops during the simulations. I'm using the very nice and powerful likwid tools to access the performance counters. Below are those measurements:

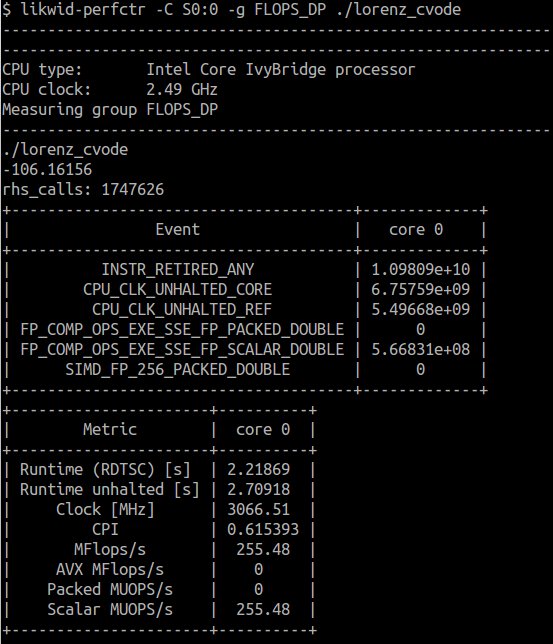
CVODE:

odeint:

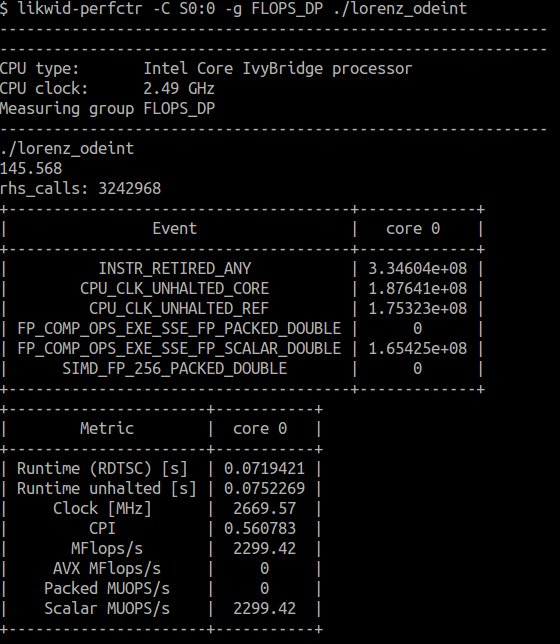
As seen in these screenshots, the odeint code produces almost 10 times the FLOPS of the CVODE version (2300 MFlops/s vs 255 MFlops/s). This is now a clear sign that the odeint-based simulation is superior: While odeint is able to make very good use of the available CPU power, CVODE has very bad CPU utilization in this example. This is probably due to being a pre-compiled library, for CVODE based code the compiler can not make use of function inlining which might result in significant performance penalties.

Analyzing the Call Graph

To follow this idea further I used the perf tool as described in Chandler Caruth's latest talk at cppcon. I'm closely following Chandler's description and first compile the binaries using -fno-omit-frame-pointer to make the stack trace available for further analysis. Then I record the benchmark using

$ perf record -g ./lorenz_cvode

which creates a benchmark report that can be analyzed with

$ perf report -g 'graph,0.5,caller'

Please watch Chandler's talk at cppcon to get some introduction on the perf tool. For CVODE I find the following performance report:

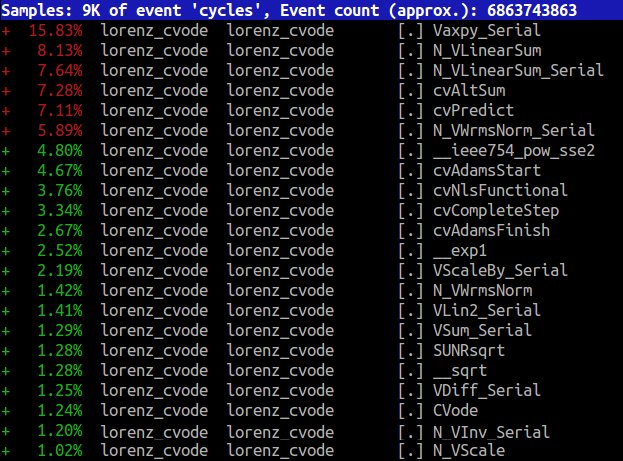
The first thing to note is that a function Vaxpy_Serial is the most time consuming function, which makes sense as this probably represents vector addition which is the core of essentially any numerical ODE algorithm. However, more importantly we find lots of functions with rather small runtime contributions. The perf report of odeint on the other hand looks very different:

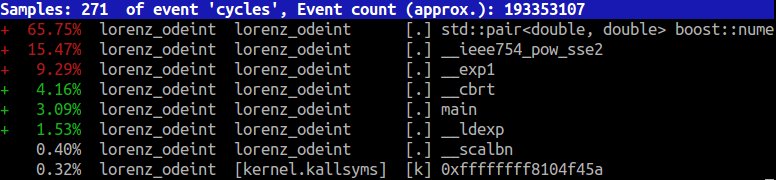
We find that 65% of the runtime is spend in a single function, the fundamental stepper function that iterates along the trajectory. All deeper numerical routines were inlined by the compiler. I strongly believe that this inlining causes the superior performance of odeint over CVODE. The Lorenz function above for example contains four additions/subtractions and five multiplications and hence should take nine CPU cycles (maybe even less). Without inlining, the additional function call probably takes as many cycles on top. Given the number of function calls within the CVODE code it is not surprising to find such a significant performance drop.

Conclusions

Function calls can turn out expensive if the actual work done within the function is very cheap. A header-only library like odeint allows the compiler to inline such functions which can result in an order of magnitude performance increase over pre-compiled libraries.

To conclude, we found that CVODE suffers from serious performance problems when dealing with small and cheap ODEs (such as the Lorenz system) due to the function call overhead. As this overhead is constant, it will become less significant for larger and more complicated ODEs. For simulating small problems, however, CVODE should not be used when optimal performance is wanted.